Soạn Toán 10 Ôn tập chương I

Ôn Tập Chương I

Bài 1: Xác định tính đúng sai của mệnh đề phủ định – A theo tính đúng sai của mệnh đề A.

Đáp án:

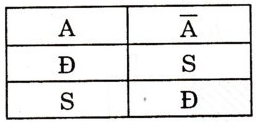
-A sai nếu A đúng

-A đúng nếu A sai

Bài 2: Thế nào là mệnh đề đảo của mệnh A ⇒ B? Nếu A ⇒ B là mệnh đề đúng, thì mệnh đề đảo của nó có đúng không? Cho ví dụ minh họa.

Đáp án :

Mệnh đề đảo của A ⇒ B là B ⇒ A

A ⇒ B đúng chưa chắc B ⇒ A đúng.

Ví dụ: A: hai góc đối đỉnh; B: hai góc ấy bằng nhau Ta có: A ⇒ B đúng. Xét B ⇒ A: nếu hai góc băng nhau thì hai góc ấy đối đỉnh. Mệnh đề này sai.

Bài 3: Thế nào là hai mệnh đề tương đương?

Đáp án:

Bài 4: Nêu định nghĩa tập hợp con và định nghĩa hai hợp bằng nhau.

Đáp án:

A⊂B ⇔ ∀x (x ∈ A ⇒ x ∈ B)

Bài 5: Nêu các định nghĩa hợp, giao, Hiệu và phần bù của hai tập hợp. Minh họa các khái niệm đó bằng hình vẽ.

Đáp án:

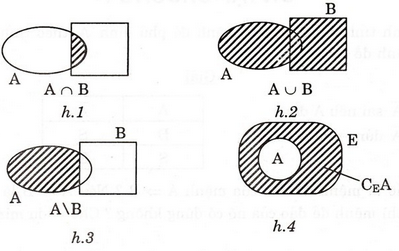
A ∩ B ⇔ ∀x (x ∈ A và x ∈ B) (h.1)

A ∪ B ⇔ ∀x (x ∈ A hoặc x ∈ B) (h.2)

A \ B ⇔ ∀x (x ∈ A hoặc x ∉ B) (h.3)

Cho A ⊂ E.CEA = {x/x ∈ E và x ∉ A} (h.4)

Bài 6: Nêu định nghĩa đoạn [a; b], khoảng (a; b), nửa khoảng [a; b), (a; b], (-∞; b], [a; +∞). Viết tập hợp R các số thực dưới dạng một khoảng.

Đáp án:

x ∈ [a; b] ↔ a ≦ x ≦ b.

x ∈ (a; b) ↔ a < x < b.

x ∈ [a; b) ↔ a ≦ x < b.

x ∈ (a; b] ↔ a < x ≦ b.

x ∈ [a; b] ↔ a ≦ x ≦ b.

x ∈ (-∞; b] ↔ x ≦ b.

x ∈ [a; +∞] ↔ a ≦ x.

x ∈ R ↔ x ∈ (-∞; +∞).

Bài 7: Thế nào là sai số tuyệt đối của một số gần đúng? Thế nào là độ chính xác của một số gần đúng?

Đáp án:

Bài 8: Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề P ⇒ Q với

a) P: “ABCD là một hình vuông”

Q: “ABCD là một hình bình hành”

b) P: “ABCD là một hình thoi”

Q: “ABCD là một hình chữ nhật”

Đáp án:

a) Đúng; b) Sai

Bài 9: Xét mối quan hệ bao hàm giữa các tập hợp sau

A là tập hợp các hình tứ giác;

B là tập hợp các hình bình hành;

C là tập hợp các hình thang;

D là tập hợp các hình chữ nhật;

E là tập hợp các hình vuông;

G là tập hợp các hình thoi.

Đáp án:

Hình vuông là hình chữ nhật …………….. nên E ⊂ D

Hình chữ nhật là hình bình hành…………….. nên D ⊂ B

Hình bình hành là hình thang…………….. nên B ⊂ C

Hình thang là hình tứ giác …………….. nên C ⊂ A

Vậy, A ⊃ C ⊃ B ⊃ D ⊃ E

Mặt khác:

– Hình vuông là hình thoi …………….. nên E ⊂ G

Hình thoi là hình bình hành………………. nên G ⊂ B

Vậy, A ⊃ C ⊃ B ⊃ G ⊃ E.

Bài 10: Liệt kê các phần tử của mỗi tập hợp sau

a) A = {3k – 2 | k = 0, 1, 2, 3, 4, 5};

b) B = {x ∈ N |x ≤ 12}

c) C = {(1 – n)n | n ∈ N}

Đáp án:

a) Khi:

k = 0 thì 3k – 2 = -2

k = 1 thì 3k – 2 = 1

k = 2 thì 3k – 2 = 4

k = 3 thì 3k – 2 = 7

k = 4 thì 3k – 2 = 10

k = 5 thì 3k – 2 = 13

Nên A = {-2; 1; 4; 7; 10; 13}

b) Vì x ∈ N và x ≦ 12 nên x = 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12

Vậy B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}

c) Vì n ∈ N nên n = 0; 1; 2;…

Do đó, (-1)n = 1 khi n = 0 hay n chẵn

(-1)n = -1 khi n lẻ

Vậy, C = {-1; 1}

Bài 11: Giả sử A, B là hai tập hợp số và X là một số đã cho. Tìm các cặp mệnh đề tương đương trong các mệnh đề sau

P: “x ∈ A ∪ B”; S: “x ∈ A và x ∈ B”;

Q: “x ∈ A \ B”; T: “x ∈ A hoặc x ∈ B”;

R: “x ∈ A ∩ B”; X:”x ∈ A hoặc x ∉ B”

Đáp án:

P ⇔ T; R ⇔ S; Q ⇔ X

Bài 12: Xác định các tập hợp sau

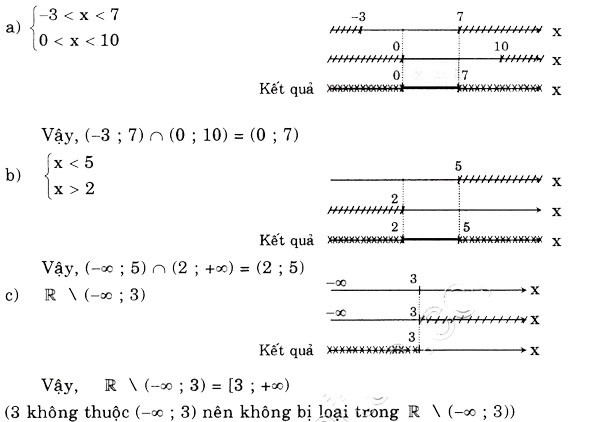
a) (-3; 7) ∩ (0; 10);

b) (—∞; 5) ∩ (2; +∞);

c) R \(—∞; 3)

Đáp án:

Bài 13: Dùng máy tính bỏ túi hoặc bảng kẻ số để tìm giá trị của 3√12 Làm tròn kết quả nhận được đến chữ số thập phân thứ ba và ước lượng sai số tuyệt đối.

Đáp án:

Kết quả đã làm tròn:

Ước lượng sai số tuyệt đối:

Bài 14: Chiều cao của một ngọn đồi đo được là h = 347,13 ± 0,2m. Hãy viết số quy tròn của số gần đúng 347,13

Đáp án:

Số quy tròn của h = 347,13 ± 0,02 (m) là h = 347.

Bài 15: Những quan hệ nào trong các quan hệ sau là đúng?

1. a) A ⊂ A ∪ B;                  b) A ⊂ A ∩ B;
2. c) A ∩ B ⊂ A ∪ B;           d) A ∪ B ⊂ B;
3. e) A ∩ B ⊂

Đáp án:

1. Đúng
2. Sai (vì X ∈ A không thể suy ra X ∈ A ∩ B)

Chúc các bạn học và thi tốt!